oscillazioni libere
circuito oscillatorio ideale
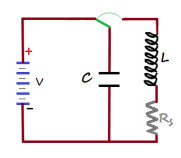
Abbiamo caricato il condensatore C collegandolo alla batteria (fig.1) e poi, una volta effettuata la carica, chiuso il circuito oscillatorio.
Vediamo di studiare analiticamente il fenomeno oscillatorio quando la resistenza Rs del circuito di fig.1 è nulla (circuito ideale).
Sappiamo che : V = tensione massima, I = corrente massima, Q = carica massima.

q = C.v; dq = C.dv; dq = I.dt;
I = C.dv/dt ,
dove i, q, v sono la corrente, la carica del condensatore di capacità C, la tensione ai capi del condensatore nell'istante t .
Possiamo scrivere che la f.e.m. indotta e nell'istante t è uguale e contraria a v, cioè: v+e = 0,
ora poiché e = L.di/dt = L.C.d2v/dt2
da questa espressione deriva che :
v = -L.C.d2v/dt2 e quindi
d2v/dt2 = - v/L.C;
la soluzione di questa equazione differenziale è:
v = V.cos (t/radq(L.C));
se poniamo 1/radq(L.C) = ω si ha :
v = V.cosωt ; da questo risultato segue:
q = C.V.cosωt; i = -C.V.ω.senωt.
Nella fig.2 è riportato l'andamento dell' oscillazione in un circuito ideale (Rs=0).
Da quanto precede possiamo quindi scrivere:
ω = 1/radq(L.C) (rad/sec) ;
f = 1/2.π.radq(L.C) (hertz);
T = 2.π.radq(L.C) (sec);
l'induttanza L è espressa in henry e la capacità C in farad.
circuito oscillatorio reale

considerando il circuito di fig.1 con Rs diverso da zero possiamo scrivere:
v+e+Rs.i = 0 e quindi:
L.C.d2v/dt2+Rs.C.dv/dt+v = 0; trattasi di una equazione differenziale completa del secondo ordine.
Se il circuito fosse ideale se cioè avesse una resistenza interna pari a zero le espressioni della corrente, della carica del condensatore e della tensione sarebbero come già visto:
v = V.cosωt ;
q = C.V.cosωt;
i = -C.V.ω.senωt.
in quanto l'ampiezza delle oscillazioni rimane costante; nel caso reale invece l'ampiezza delle oscillazioni varia con una legge rappresentata graficamente in fig.3 dalla linea tratteggiata.
se riusciamo a determinare tale legge che chiamiamo f(t) possiamo scrivere le espressioni di i, q e v di un circuito reale, come segue:
v = V.f(t).cosωt ;
q = C.V.f(t).cosωt;
i = -C.V.f(t).ω.senωt.
Per ricavare la f(t) prendiamo in considerazione la linea tratteggiata di fig.3.
Possiamo dire che lungo tale curva tutta l'energia posseduta dal sistema corrisponde all'energia della bobina essendo lungo tale linea il condensatore scarico, cioè tutta l'energia si è trasformata in energia magnetica.
Sappiamo che l'energia magnetica lungo tale linea tratteggiata è pari a 1/2.L.I2
e quindi la perdita di energia passando dal punto 1 al punto 2 è pari a :
L/2(I12-I22); tale energia si è trasformata in calore nella resistenza Rs e cioè essa è diventata uguale a Rs I12eff.T/2 ; se supponiamo che lo smorzamento non sia eccessivo, come spesso capita in pratica, possiamo scrivere :
I12eff = I1/radq(2) ; allora sarà:
(I12-I22).L/2 = (Rs.I12/2).T/2 ; 1-(I22/I12 ) = Rs.T/2L.
analogamente possiamo scrivere:
1-(I22/I12) = 1-(I32/I22) = 1-(I42/I32) = 1-(I52/I42) = ......... = Rs.T/2L. e quindi:
I22/I12= I32/I22= I42/I32= I52/I42 .............; e anche
I2/I1 = I3/I2 = I4/I3 = I5/I4 ....................; da ciò deriva che:
I22= I1.I3 ; I32= I2.I4 ; I42= I3.I5 .................;
I32= I1.I5 ; I42= I2.I6 ; I52= I3.I7..................;
da queste ultime espressioni si deduce che il valore massimo di una qualsiasi ampiezza è medio proporzionale fra due qualsiasi valori massimi equidistanti.
L'espressione di sopra:
1-(I22/I12) = RsT/2L , perquanto detto, può scriversi in questo modo:
1-(I1-I3)/I12 = (I1-I2)/I1 = Rs.T/2L.
Nel tempo T la corrente cresce del valore -(I1-I3) = (I3-I1); nel tempo dt crescerà del valore -di/i = Rs .dt/2L; ponendo α = Rs/2L ed integrando abbiamo:
ln i = -αt + lnk ; per t = 0 ed i = I0 si ha: ln I0 = ln K da cui K = I0.
si ha allora:
ln I/I0 = -αt e pertanto e -αt = I/I0 e quindi i = I0.e-αt;
la nostra f(t) cercata è pertanto uguale a I/I0 = e-αt = e -(Rs/2L)t e quindi per un circuito reale le espressioni della corrente è la seguente:
i = -C.V.e-(Rs/2L)t.ω.senωt .
Per analogia le espressioni della tensione e della carica del condensatore sono:
v = V.e-(Rs/2L)t.cosωt
q = C.V.e-(Rs/2L)t.cosωt;
Inoltre dalla risoluzione dell'equazione differenziale del circuito risulta :
ω=radq(1/LC -α2) = radq(1/LC - Rs2/4L2), da cui
T= 2.π/ω =2.π/radq(1/LC-Rs2/4L2).
Per Rs = 0 (oscillatore ideale) si ottiene l'espressione nota:
T=2.π.radq(LC).
decremento logaritmico
da quanto detto risulta che il rapporto In/In+2 è costante (vedi fig.3); In ed In+2 sono due massimi che distano di un periodo.
Questo rapporto è pari α eαt infatti se facciamo il rapporto fra :
I1 T = -C.V.e-(Rs/2L)T.ω.senωT e I2T = -C.V.e-(Rs/2L)2T.ω.senω2T
otteniamo appunto I1 T/I2T = In/In+2 = eαt .
Il logaritmo neperiano di questo rapporto si chiama decremento logaritmo e viene indicato con la lettera greca δ esso serve per confrontare due oscillazioni aventi differente smorzamento ed è pari a:
ln(In/In+2) = ln(I1T/I2T) = αT = RsT/2L ;
da questa espressione si ricava, nell'ipotesi che Rs sia piccolo tale che T possa ritenersi pari a 2.π.radq(LC) :
δ=π.Rs.radq(C/L).
Questa espressione ci dice che a parità di Rs è opportuno diminuire C ed aumentare L per diminuire il decremento logaritmo.
La presenza della resistenza ohmica nel circuito determina lo smorzamento causando una perdita di energia ; se noi somministriamo al circuito con continuità l'energia che viene perduta otteniamo delle oscillazioni persistenti;
In questo caso il decremento logaritmico rappresenta il rapporto ΔW/W dove ΔW è l'energia persa nel semi periodo e W l'energia totale posseduta dal circuito. I
Infatti posso scrivere:
W = LI2/2;
ΔW = RsIeff2.T/2 = Rs (I2/2).T/2, e quindi
ΔW/W= RsT/2L = δ .
Quindi posiamo dire che nel caso delle oscillazioni persistenti il decremento logaritmico rappresenta la quantità di energia che in ogni semi periodo devo somministrare per mantenerle tali.
resistenza critica
Abbiamo visto che il periodo in un circuito oscillatorio reale è:
T=2π/ω = 2π/radq(1/LC - Rs2/4L2).
Si osserva che tale periodo è più lungo di quello del circuito ideale che ha la medesima induttanza e capacità.
T diventa infinito quando ω = 0 cioè quando 1/LC = Rs2/4L2 e quindi Rs=2radq(L/C).
Questo valore della Rs si chiama resistenza critica.
Allora possiamo scrivere:
Rs<2radq(L/C) circuito oscillatorio smorzato;
Rs>2radq(L/C) circuito aperiodico;
Rs=2radq(L/C) condizione limite fra le due precedenti;
La Fenice rinasce dalle proprie ceneri
Il tuo sito senza pubblicità?
Puoi con JimdoPro e JimdoBusiness!
La dritta


