OSCILLATORI
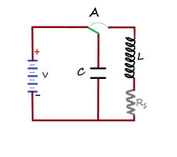
Abbiamo visto quando abbiamo parlato dei circuiti oscillatori che se, dopo aver caricato il condensatore C di fig.1, chiudo il circuito risonante ruotando verso destra l'interrutore A , il condensatore inizia a scaricarsi attraverso l'induttanza e genera una corrente alternata sinusoidale la cui frequenza f dipende dal valore di C e di L .
La presenza della resistenza interna Rs del circuito determina uno smorzamento delle oscillazioni che mantengono la frequenza costante ma vanno diminuendo in ampiezza fino a cessare del tutto., come si nota in fig.2

Ad ogni ciclo il sistema perde energia e l'ampiezza dell'oscillazione diminuisce sempre più; cioè alla fine di ogni ciclo il condensatore si carica sempre di meno finchè non si carica per nulla e le oscillazioni cessano.
Se voglio ottenere delle oscillazioni persistenti devo trovare un modo di restituire al sistema oscillatorio l'energia che perde ad ogni ciclo.
Cioè dovrei trovare un sistema che mi permetta di spostare verso sinistra con la frequenza f l'interrutore A di fig.1 fino a caricare il condestatore C in modo che esso raggiunga la tensione della batteria alla fine di ogni ciclo e poi rispostarlo verso destra.
Cioè l'energia deve essere fornita con la stessa frequenza, in fase e con ampiezza adeguata.
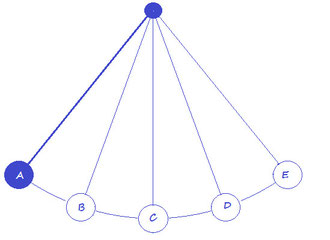
Il nostro circuito oscillatorio si comporta esattamente come un pendolo (fig.3)
Se metto la sfera nella posizione A e la lascio andare essa si porterà dopo un certo periodo di tempo nella posizione E poi invertirà il suo cammino e si dirigerà verso A.
Durante questo tragitto perderà energia e non arriverà esattamente nella posizione A ma raggiungerà, per esempio, la posizione B molto prossima ad A.
Raggiunta tale posizione invertirà il senso di marcia ed arriverà nel punto D molto prossimo ad E .......insomma l'oscillazione si smorzerà sempre più finché la sfera non si fermerà portandosi nella posizione di riposo C.
Se Voglio mantenere l'oscillazione persistente dovrò agire in questo modo:
Quando la sfera, dopo aver raggiunto la posizione, E avrà invertito il cammino e sarà ritornata in una posizione prossima ad A (per esempio B) dovrò dare alla sfera un impulso rivolto verso E (in fase con l'oscillazione); l'impulso dovrà essere (adeguato) tale da ridare alla sfera l'energia persa nel tragitto fra A-E-A (B) ed inoltre l'impulso dovrà essere dato ogni volta che la sfera giunge in A (B), cioè con la stessa frequenza dell'oscillazione.
Tornando al nostro circuito oscillante ,non posso certamente pensare di progettare un sistema meccanico che mi permetta di chiudere l'interruttore A ogni volta che è necessario, infatti le nostre oscillazioni sono molto elevate è ciò non è possibile.
Si può però ricorrere ad un sistema elettronico che provveda ad azionare il nostro interruttore con la dovuta frequenza, in fase con l'oscillazione e fornendo un'adeguata energia.

Il sistema elettronico che utilizziamo è un triodo (fig.4); vediamo come funziona.
Una perturbazione qualsiasi, che di solito nasce spontaneamente, fa oscillare il circuito oscillatorio L1-C ; tale oscillazione si smorzerebbe in breve tempo se non intervenisse il triodo.
L'oscillazione sorta spontaneamente nel circuito L1-C induce nel circuito di entrata L2 una tensione oscillatoria che iniettata nella griglia viene amplificata dal triodo.
Parte della tensione oscillatoria amplificata che si trova nella placca, se di fase appropriata e se l'accoppiamento fra L3ed L1 è sufficiente induce nel circuito oscillatorio (reazione positiva) una tensione tale da riportare il secondo periodo dell'oscillazione alla medesima ampiezza del primo e così di seguito.
Nel caso di fig.4 il circuito L1-C è separato dal resto; di solito invece capita che esso fa parte del circuito anodico o di quello di griglia oppure di entrambi.
Il circuito di fig.4 è molto teorico e fa più o meno capire come funziona un oscillatore. In fig.5 è disegnato un circuito che ha molta più attinenza con la realtà e che ci fa capire meglio il funzionamento degli oscillatori.
Intanto osserviamo che il triodo (1) di fig.5 così come montato funge da amplificatore, Se unisco il punto B col punto A il circuito potrebbe oscillare se il segnale Ve fosse in fase col segnale V1...ciò però non avviene in realta; V1 e V2 sono sfasati.
Perchè avvenga l'oscillazione occorre allora trovare un modo per rendere il segnale entrante in fase con quello escente.
Ciò è possibile aggiungendo un altro amplificatore come in fig.5 (2)
L' oscillatore di fig.5(3) è un moltivibratore astabile che produce oscillazioni di rilasciamento ; si chiama oscillatore di Abraham.
Vediamo come funziona:
Un impulso positivo dato alla griglia di T1 viene amplificato e si ritrova in opposizione di fase (negativo) nell'anodo di T1 ,
tale segnale negativo viene portato nella griglia di T2 tramite il condensatorte C2, dalla griglia di T2 passa , amplificato e cambiato di segno (positivo) nell'anodo di T2; attraverso C1 viene portato alla griglia di T1 e dopo l'amplificazione passa all'anodo di T1 cambiato di segno ( negativo) .
Si ha dunque una continua amplificazione del segnale con la griglia di T2 che diventa sempre più nagativa.
E' evidente che l'amplificazione non può continuare all'infinito; infatti quando la griglia di T2 assume un potenziale negativo corrispondemnte all'interdizione l'amplificazione si interrompe inquanto nel triodo T2 cessa la circolazione della corrente.
A questo punto la corrente anodica continua in T1 ed il condensatore C2 si scarica attraverso R2 facendo aumentare la polarizzazione della griglia di T2 (diventa senmpre meno negtiva) e facendo quindi riprendere la circolazione nel triodo T2. La circolazione della corrente in T2 fa diminuire la tensione anodica di T2 ( caduta nella resistenza R4) ciò determina un impulso negatico nella griglia di T1 che amplificato e cambiato di segno (positivo) passa nell'anodo di T1 , dall'anodo di T1 passa attraverso C2 alla griglia di T2 poi amplificato e cambiato di segno (negativo) all'anodo di T2 poi attraverso C1 alla griglia di T1 che diventa sempre più negativa fino ad arrivare alla interdizione ......il processo continua ... T1 e T2 conducono alternativamente e si forma un'nda quadra.
In realtà anchè con un solo amplificatore è possibile ottenere un oscillatore a patto che il segnale in uscita venga reso in fase con quello in entrata, e ciò si può fare se aggiungiamo un marchingegno al circuito com riportato in fig.6 (4).
gli schemi di fig.5 e fig.6 mostrano degli amplificatori non selettivi e con essi possiamo ottenere degli ascillatiri aperiodici non sinusoidali (onda più o meno quadra).
Le frequenze ottenibili con tale sistema non sono molto elevate.
E' evidente che affinchè l'oscillazione avvenga e sia persistente non è sufficiente che il segnale uscente riportato in entrata sia in fase col segnale in entrata, occorre ancne che la potenza conferita dal tubo al circuito oscillante sia maggiore di quella da esso dissipata.
Siamo in presenza di generatori.
Quando abbiamo parlato di reazione positiva abbiamo detto che l'amplificazione con reazione è pari a : Ar=A/1-βA = VU/ VI e che se si verifica 1 - βA = 0 ( condizione di Barkhausen ) sarà Ar= VU/ VI = oo.
Ciò significha o che VU = oo con VI diverso da zero oppure che Vi = 0 con VU diverso da zero.
Il primo caso è fisicamente impossibile , è invece possibile avere un segnale in uscita diverso da zero con un segnale in ingresso nullo cioè un generatore.
Concludiamo dunque che per avere un circuito generatore (oscillatore) occorre che si verifichi la condizioone di Barkhausen 1 - βA = 0.
OSCILLATORI A RADIO FREQUENZA
Se invece di considerare degli amplificatori aperiodici partiamo da amplificatori selettivi e colleghiamo l'uscita con l' ingresso del segnale, rispettando le condizioni di concordanza di fase, e purchè l'amplificazione sia sufficiente si generano ancora delle oscillazioni che risulteranno sinusoidali .Partendo dunque da amplificatori selettivi possiamo ottenere vari tipi di oscillatori .
I più noti sono:
- Oscillatore di Armstrong
- Oscillatore di Meissner
- Oscillatore di Reinardz
- Oscillatore di Hartley;
- Oscillatore di Colpitts;
Oscillatore Armastrong
accoppiamento per capacità interna ( -Cag- anodo-griglia)
Nel circuito di Armstrong di fig. 6a la retrocessione del segnale dall'uscita all'entrata avviene attraverso la capacità interna Cga.
La tensione va (va deriva dalla tensione applicata alla griglia amplificata e in opposizione di fase con essa) presente nell'anodo determina il passaggio della corrente Iga attraverso la capacità Cga che anticipa la tensione va di 90° (vedi figura 6a (b).
La corrente Iga attraversa anche il circuito L1 C1 e determina ai suoi capi una tensione v'g ; se questo circuito ha un comportamento induttivo la Iga risulta in ritardo rispetto a v'g di 90° (vedi deisegno 6a (b).
In queste condizioni dal disegno 6a(b) si nota che v'g e va sono in opposizione di fase e quindie quindi v'g e vg sono in fase come deve essere perchè il circuito possa comportarsi da generatore.
I circuiti L1C1 e L2C2 non devono influenzarsi e devono essere montati con gli assi perpendicolari fra loro o, meglio, schermandoli con schermi in alluminio o rame.
L'oscillatore di Armstrong è particolarmente adatto per le alte frequenze poichè a tali frequenze la reattansa di Gga è molto bassa.
Qualora il valore di Cga non fosse sufficiente per l'innesco delle oscillazioni si può inserire fra anodo e griglia (in parallelo con Cga) un condensatore di piccolo valore.
Oscillatore di Meissner
accoppiamento per mutua induzione

Ll'oscillatore fa parte del circuito di placca.
fra circuito risonante e induttanza di reaziome si ha un accoppiamento per mutua induzione.
La resitenza R' ed il condensatore C' costituiscono il gruppo di polarizzazione automatica.
Le formule per il calcolo dell'oscillatore di MEISSNER sono le seguenti:
- f0= 1/2π√(LC);
- M=(1/gm)(1/Rp) = K√L'L
K è il coefficiente di accoppiamento che poniamo pari a 1 supponendolo molto stretto.
La formula della frequenza di risonanza f0 deriva dall'eguaglianza della impedenza della bobina L (XL= 2πf0L) e del condensatore C (XC= 1/2πf0C).
per quanto riguarda M possiamo scrivere:
β = Vr/Vu dove Vr= -J ωMI ; ed I=Vu /JωL
Sostituendo il valore di I si ha:
Vr= -J ωMVu / J ωL : Vr/Vu = β = -M/L
poichè l'amplificazione di uno stadio con carico Z , come per il caso dell'oscillatore di Reinartz, in condizioni di risonanza, è dato da :
A=-gm Z = -gm x Rp , si ha , applicando la condizione di BARKHAUSEN,
β A = M/L x gm x Rp = 1
e quindi risulta M= 1/gm x L/Rp
Oscillatore di Reinartz
accoppiamento per mutua induzione

Questo circuito è molto simile all'oscillatore di Meissner,
In questo caso il circuito risonante fa parte del circuito di griglia.
La tensione oscillante sinusoidale prodotta dal circuito L1-C1, che si eccita spontaneamente all'accensione del triodo, attraverso il condensatore C2 giunge nella griglia del triodo e quindi viene amplificata.
parte di questa tensione viene retrocessa dalla placca alla griglia tramite l'induttanza L2 che induce in L1 una tensione che provvede a caricare il condensatore C1 portando la sua tensione al valore che aveva all'inizio del ciclo; il processo, in determinate condizioni, continua all'infinito.
E' evidente infatti che affinché l'oscillazione si auto-sostenga occorre che la tensione retrocessa sia in fase con la tensione oscillante prodotta da L1-C1, abbia la stessa frequenza e sia di opportuna ampiezza in modo da ridare al sistema L1-C1 l'energia persa durante ogni ciclo.
Il circuito di fig. 5 (a) è alimentato in parallelo; in esso il condensatore C3, di elevato valore al fine di non rappresentare una elevata impedenza alle componenti alternative, ha la funzione di evitare che la batteria risulti in corto circuito, e l'induttanza L3,che deve avere una impedenza elevata alla radio frequenza, favorisce il suo passaggio verso il condensatore C3 per un ottimale funzionamento del sistema.
Ponendo la batteria fra la placca e l'induttanza L2 oppure fra l'induttanza L2 e massa e togliendo il condensatore C3 e l'induttanza L3, come è mostrato in fig.5 (b) ed in fig.5(c) , il circuito risulta alimentato in serie.
La reazione è regolata variando la posizione della bobina di reazione rispetto alla bobina dell'oscillatore.
La resitenza R1 ed il condensatore C2 costituiscono il gruppo di polarizzazione automatica.
Le formule per il calcolo dell'oscillatore di REINARTZ sono le seguenti:
- f0 = 1/2π√(L1C1);
- M = L2 x Rp/Ri .
La formula della frequenza di risonanza f0 deriva dall'eguaglianza della impedenza della bobina L1 (XL= 2πf0L1) e del condensatore C. (XC= 1/2πf0C1).
per quanto riguarda la seconda formula, evidenziando che Ri è la resistenza interna del triodo ed Rp il parallelo fra la resistenza dinamica del circuito oscillatorio e la resistenza Ri, per la sua dimostrazione , possiamo scrivere:
Vr = JωL2 I da cui I = Vr/JωL2; (Vr è la tensione ai capi della bobina di reazione L2)
Vgk = -Jω M I = -Jω M Vr/JωL2 ;
Vu= Vgk x μ = -Jω μ M Vr/JωL2 = -μ M Vr/L2 ; poichè β = Vr/Vu si ha :
1 = - μ M Vr / VuL2 = - μ β M/L2 da cui β = -(1/ μ)L2/M
La condizione di Barkahusen dice che βA=1
dove A è il guadagno pari a A = -gm x Rp.
come indicato sotto in fig. 6 :
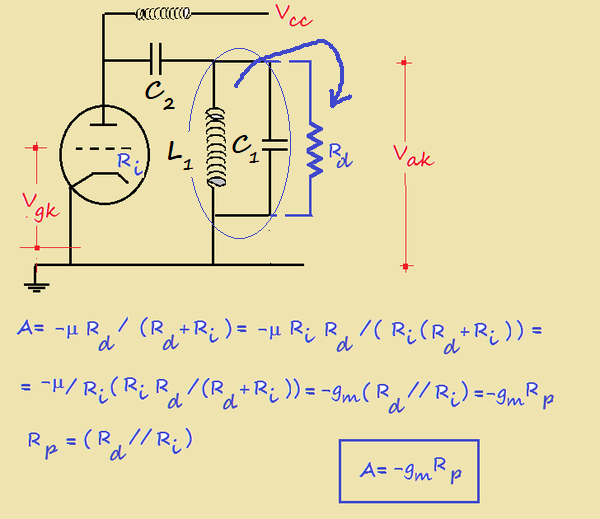
A altro non è che l'amplificazione a catodo comune, come nel nostro caso.
In fig.6 si nota come nell'amplificazione in condizioni di risonanza il nostro circuito L1L1 è come se venisse sostituito dalla resistenza dinamica Rd che risulta in parallelo alla resistenza interna del tubo Ri.
applicando il principio di Barkahusen si ha dunque:
β x (-gm x Rp) = 1
sostituendo il valore di β = -(1/ μ)L2/M
risulta si ottiene : M = L2 x Rp/Ri
Oscillatore di Hartley
accoppiamento per autoinduzione
E' un oscillatore a tre punti: i tre punti sono la placca, la griglia ed il catodo.
Nella figura 9 sono indicate tre soluzioni circuitali.
La resistenza R2 ed il condensatore C2 di fig. 9 hanno la funzione, come nei casi su trattati, di polarizzare la griglia del triodo.
Le relazioni fondamentali per la progettazione di un oscillatore di hartley sono:
- f0 = 1/2π√(L0c1);
- L0 = L1 +L2+2M;
- (L2 + M)/(L1+ M))x gm x Rp=1
Rp è la resistenza dinamica Rd = ωL0Q del circuito risonante in parallelo con la resistenza interna del tubo.
Cioè Rp = (Rd x Ri)/(Rd + Ri)
La formula della frequenza di risonanza f0 deriva dall'eguaglianza della impedenza della bobina avente induttanza L0 (XL0= 2πf0Rp) e del condensatore C. (XC= 1/2πf0C).
L0 è l'induttanza delle due bobine in serie L1 ed L2 che è pari alla somma delle due induttanze L1 ed L2 e del doppio della muta induttanza M.
Per quanto riguarda la terza formula ricordando le espressioni:
- Vak= Jω0(L1+M) x I;
- Vgk= Jω0(L2+M) x I;
- β = -Vgk/Vak;
- A= - gm x R;
- βA=1
si ricava facilmente l'epressione: (L2 + M)/(L1+ M))x gm x Rp=1
Oscillatore di Colpitts
accoppiamento per capacità
E' un oscillatore a tre punti: i tre punti sono la placca, la griglia ed il catodo.
L'alimentazione del circuito è in parallelo; il circuito oscillante di Colpitts non può essere alimentato in serie, cioè con la batteria posta tra la placca e il circuito oscillante, perchè in questo caso il circuito della corrente continua non risulterebbe chiuso.
La reazione è regolata variando la capacità dei due condensatori C1' e C1''
La resitenza R2 ed il condensatore C2 costituiscono il gruppo di polarizzazione automatica.
Le formule per il calcolo dell'oscillatore di COLPITTS sono le seguenti:
- f0= 1/2π√(L1C);
- C = C1' . C1''/ ( C1'+ C1'' ) (sono i due condensatori C1' e C1'' in serie)
- C1'' / C1' x gm x Rp = 1
gruppo di polarizzazione

Tutti gli oscillatori su rappresentati hanno lo stesso gruppo di polarizzazione di griglia (fig.9b); vediamo come funziona:
Il condensatore C serve ad isolare la griglia in modo che il suo potenziale medio possa essere diverso da quello del catodo, cosa impossibile senza di esso poiché griglia e catodo sono tra loro collegati attraverso l'induttanza che fa appunto parte del circuito di griglia.
La corrente di griglia è costretta ad attraversare la resistenza R nel senso indicato in figura e determina pertanto una caduta di tensione che polarizza la griglia negativamente.
Tale polarizzazione evidentemente non è pulsante, come sembrerebbe a prima vista, perché il condensatore C funge da volano, si carica cioè quando la corrente di griglia ha valore maggiore del suo valore medio e si scarica, mantenendo a sue spese la corrente nella resistenza R e quindi anche la tensione di polarizzazione, allorché la corrente di griglia è nulla o comunque minore del suo valore medio.
Affinché la tensione di polarizzazione sia praticamente costante occorre che la costante di tempo RC sia molto maggiore del periodo delle oscillazioni, cioè RC>>T.
Ora, fissato R in base al valore medio della corrente di griglia ed alla polarizzazione che si vuole ottenere , conoscendo L0 e C0 , induttanza e capacità del circuito oscillatorio, ponendo R C >= 10T ottengo la capacità del condensatore C, in tal modo:
C>= (10. 2π RADQ(C0 L0))/R.
Si osserva che in tal modo il potenziale di polarizzazione si stabilisce solo quando nasce la corrente di griglia, mentre inizialmente esso è nullo, e l'innesco sarà pertanto facile.
Il valore di R si aggira fra i 1.000Ω ed i 100.000Ω.
Le due configurazioni (a) e (b) di fig.9b sono identiche.
OSCILLATORI A BASSA FREQUENZA
Oscillatore di WIEN

L'oscillatore di Wien è costituito da da un amplificatore a due stadi per ottenere uno sfasamento del segnale uguale a zero ed ha una reazione positiva ed una negativa .
in fig. 10 in verde è indicata il circuito di reazione negativa ed in azzurro quella di reazione positiva.
Le formule relative al circuito sono:
- f0 = 1/2πRC;
- 2R2= R1;
- A>=3.
In fig.10 a) c'è una rappresentazione chiara del ponte di Wien.
Facendo riferimento a questa figura possiamo scrivere:
- Z1 : Z2 = Zs : Zp
che equivale alla :
- Zs x Z2 = Zp x Z1
poichè Z1= R1 ; Z2= R2; Zs = R-J1/ωC ; Zp = -(JR/ωC) / (R-J/ωC),
con alcuni passaggi otteniamo:
R2 R2 - R2/ω2 C2 - J2RR2/ωC = -JRR1/ωC da cui risulta :
R2 R2 - R2/ω2 C2 = 0
e quindi : R2ω2 C2 = 1 da cui risulta f0 = 1/2πRC;
risulta anche - J2RR2/ωC = -JRR1/ωC e quindi 2R2=R1
poichè β= R2 / R2+R1 = R2 / R2+2R2 = 1/3
la condizione di Barkahusen A β =1 ci porta a scrivere : A=3
Oscillatore a sfasamento

E' un oscillatore molto stabile ma poco usato nelle strumentazioni per le difficoltà della modifica della frequenza generata (diversamente dall'oscillatore di Wien).
L'oscillatore è costituito da una rete di sfasamento a tre celle che sfasano il segnale di 60° ciascuna.
Quindi dalla griglia alla placca ho uno sfasamento di 180, dalla placca alla griglia uno sfasamento di 60° x 3 = 180, ; totale 360 °
Il segnale rientra in griglia sfasato di 360° e quindi in fase.
Le formule relative al circuito sono:
- f0 = 1/2π(√6)RC;
- A>=29
Per ottenere le formule si applica il 2 ° principio fo Kirkoff alle maglie:
- Vu = (Xc+R) i1 - R.i2 ;
- 0 = (2R+Xc) i2 - i1 R - i3R;
- 0 =(2R + Xc) i3 - i2R.
Da queste tre equazioni si ricava i3 e quindi Vr e quindi
β = Vr / Vu
1/ β = (1- 5 /ω02 C2 R2) + (1/Jω0 C R) (6- 1/ω02 C2 R2);
Poiché per la condizione di Barkhausen Aβ=1 , A è reale e negativa , anche β deve essere reale e negativo perciò deve essere (6- 1/ω02 C2 R2);= 0 e cioè:
6 ω02 C2 R2 = 1 da cui si ricava f0 = 1/2π(√6)RC;
ora l'espressione 1/ β può essere scritta essendo la parte immaginaria uguale a zero in tal modo:
1/ β = -1/29 e cioè A = 29
La Fenice rinasce dalle proprie ceneri
Il tuo sito senza pubblicità?
Puoi con JimdoPro e JimdoBusiness!
La dritta







